Pyrolysis is the degradation of a substance by thermal energy in an inert atmosphere. The process generally follows a first-order reaction, that is the degradation, or alternatively the formation of pyrolysis products, is proportional to the amount of sample that has not reacted yet. The result is a curve that is decreasing exponentially, as shown in figure 1.

The degradation rate is highly dependent of temperature. Thus a small increase in temperature will have a large influence on how fast a substance is pyrolysed. In the example the time to pyrolyse the polymer PMMA is decreased by a factor of five when the temperature is increased 40°C. The degradation rate is conveniently characterized by the reaction half-life, t½, which is the time for half of the remaining substance to react, see the figure.

Furthermore, the temperature dependence of the reaction rate generally follow the Arrhenius equation, which gives a linear dependence of the logarithm of the reaction rate k vs. the inverse temperature, see figure 2. This diagram shows the temperature dependence of the reaction rate, i.e. the formation of monomers by pyrolysis, of 5 different polymers.

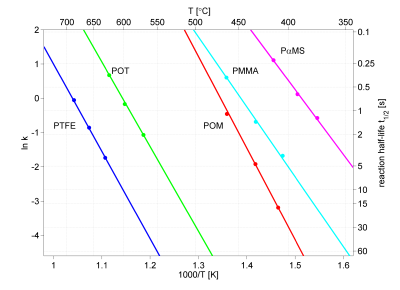
Two alternative scales are given for easier interpretation, the pyrolysis temperature in °C on the top of the diagram, and the reaction half-life t½ to the right. Note the rapid decrease in half-decomposition time with increasing temperature.

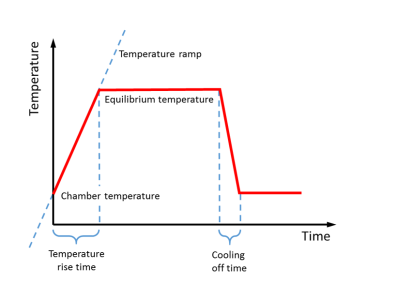
However, the temperature is not increased momentary. Rather it follows a temperature time profile, see figure 3. The temperature starts at a chamber temperature, increases to the equilibrium temperature, or final pyrolysis temperature. The time it takes is called the temperature rise time. The temperature increase may also be characterised by the temperature ramp, in °C/s. The temperature is held constant, and then decreases during the cooling of time.

The influence of the temperature rise time may be investigated by a numerical experiment. This work was presented at the Pyro2016 conference in Nantes, France, see this link.

These are the assumptions:

• The pyrolysis is a first-order reaction.
• The reaction rates given by the Arrhenius equation are valid for all temperatures.
• The temperature is the same in the whole sample and follows a given temperature time profile.

With these assumption the thermal degradation of the polymer PMMA is calculated for a normal isothermal pyrolysis with 8 ms temperature rise time, and three different temperature ramps. The result is shown in figure 4. The temperature time profile and the formation of pyrolysis products are shown in the same diagram.

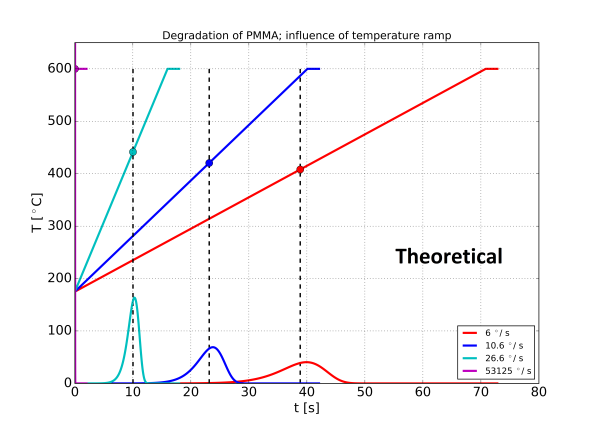
Two effects may be observed: With the slower temperature ramps the sample is pyrolysed before the equilibrium temperature is reached. A slower ramp also has the consequence that the pyrolysis products are formed at a lower intensity over a longer period of time, making the peaks wider.

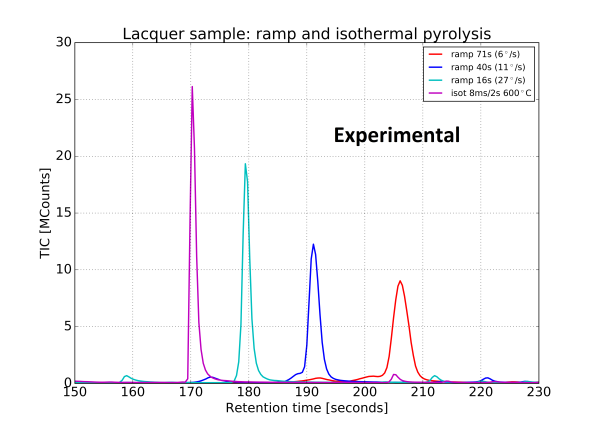
An experiment was then performed under the same conditions, the result is shown in figure 5. The widening of the peaks was confirmed.

Summary

• In order to get a well-defined pyrolysis temperature it is important to have a short temperature rise time. A slow rise in temperature will cause the substance to be pyrolysed before reaching the final pyrolysis temperature, and the actual pyrolysis temperature will depend on the temperature ramp. 
• In order to get a well-defined pyrolysis temperature it is important to have a the same temperature throughout the sample. This implies small sample sizes.
• In order to stop the pyrolysis of the sample it is important to have a very rapid cooling, and to decrease the temperature well below the pyrolysis temperature.